29 April 2025

Sam Thompson
Engineering Manager
Selecting tooth counts is one of the key decisions to be made at the early stages of any gearbox design. For a simple gear pair the maths and the scale of the problem is easily bound, enabling an experienced designer to make decisions and understand trends with relative ease. If we have flexibility over the centre distance and rack tooling then the key considerations are the selection of a hunting ratio and the desire to avoid any common factors that may lead to potential excitations. The problem gets a little more involved if we need to design around standard racks or existing centre distances as we need to making decisions on how much profile shift we can tolerate when drifting away from the ideal module. Ultimately however, if the tooth counts satisfy the ratio requirement then the gear pair will at least assemble and function. This is not the case for planetary gear trains which require a lot more thought when selecting tooth counts as shown in the image below, which highlights just some of the design decisions that have to be made.

Let’s consider a simple epicyclic with a 5:1 ratio. Using some very typical tooth count limitations to initially bound the design space, the number of theoretical candidates that satisfy the ratio requirement is 77. However, only 24 of these are viable when the planetary assembly condition is considered but the problem does not stop here. Of those 24, only 12 will fit within our package volume and ensure no planet gear tip-to-tip clashes (this becomes particularly challenging with increased numbers of planets and high ratio requirements). We are now left with only 15% of the original 77 possible candidates. If we consider additional requirements like the desire to have a fully factorising gear train, the number of candidates reduces to just six or only 7% of the original design space!
Even the most experienced gear designer cannot be expected to identify six candidates from a possible 77. Using Hewland’s in-house tools, we can add additional functionality like the ability to calculate component speeds which must not be overlooked due to the significance of centrifugal loads. It is even possible to add early mass estimations based on a torque requirement and the minimum facewidth needed to achieve a certain bending strength.

Figure 1: Possible tooth counts for a simple epicyclic
That was for a simple planetary system, now let’s focus our attention on a compound planetary gear train where the scale of the problem becomes orders of magnitude more complex. At this point it’s worth reminding ourselves of the fundamental ratio equation for a compound planetary system:


The ratio calculation is inherently more complex as it is driven by the tooth counts of all four gear members, which increases the design space significantly. Again, it’s worth looking at some numbers to demonstrate the scale of the challenge. To perform a full factorial sweep of 25 tooth counts options for each gear member requires a design space of over 390,000 (25^4) candidates – this is beyond what is practically manageable in Excel. We therefore must do some intelligent pre-processing to reduce the design space by removing tooth counts that do not meet certain criteria (such as the requirement for hunting ratios). This reduces the design space down to a more modest 63,750 candidates. From here it is possible to start filtering out candidates that do not meet our criteria as described by the flow chart opposite, which shows that just 0.2% of the design space remains once all filtering is applied.
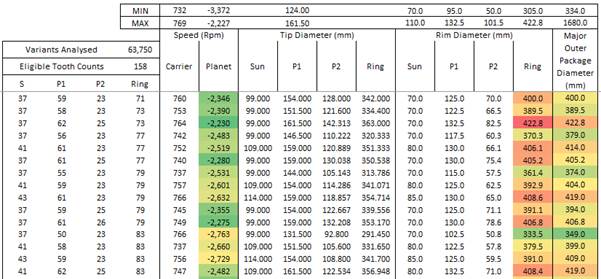
Figure 2: Possible tooth counts for a compound planetary
At this point it is worth talking about the unique complexity of compound planetary systems which centres around their manufacture and assembly. Depending on the tooth counts of the individual members, it may be necessary to perform special alignment during both manufacture and assembly. During manufacture it may be required to align the driving flanks of the compound planetary gears to each other and include a special identification feature on these aligned teeth. Furthermore, during assembly a specific amount of rotation of the identified teeth may be required to enable assembly of all the planet pins. Both of these requirements add considerable complication to both the manufacturing and assembly processes, however this can all be avoided by careful selection of the tooth counts.
As a transmission designer, I want to spend more of my time on the more complex job of optimising the transmission system in terms of durability, weight and efficiency. I want to avoid spending time searching for and deliberating over potential tooth counts as this is largely a question of geometry and can be automated via Excel or similar. By using Hewland’s bespoke tooth number generators, I can see all available options and visualise trends in a matter of minutes to help me make the most appropriate selections, ensuring the system design gets off to the best start.

Figure 3: Spotting trends within compound planetary tooth counts
If you’re finding the task of selecting planetary tooth counts daunting, give us a call and we can collaborate to develop your solution!